Binary Search - Tìm kiếm nhị phân
---
---
Giới thiệu bài toán
Thuật toán truyền thống
Tối ưu
Trong thực tế nhiều trường hợp, chúng ta luôn phải sắp xếp, tìm kiếm theo một chuẩn nào đó. Ví dụ như:
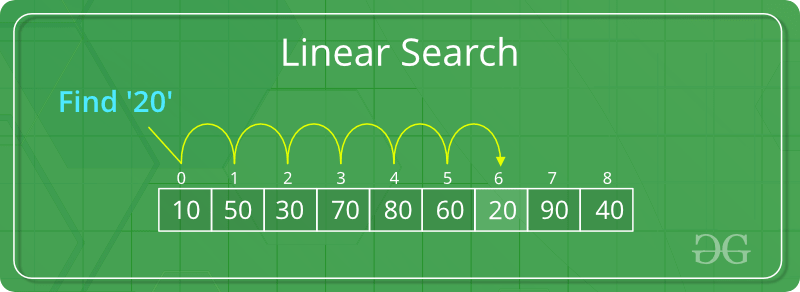
Tất cả chúng ta đều biết rằng, muốn tìm kiếm một sinh viên nào đó trên bảng danh sách thì cách đơn giản nhất đó là : “Đi từng sinh viên từ đầu, kiểm tra xem đó có phải sinh viên cần tìm không, không thì next”.
Ví dụ chúng ta có mảng A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9} với Key = 7
Theo đúng cách trên thì ta có cách duyệt từ đầu đến cuối. Nếu giá trị mình cần tìm là Key thì sẽ in ra vị trí xuất hiện đó
Về thuật toán tối ưu sự tìm kiếm thì có một thuật toán kiểu : “À mày không phải cái ta tìm kiếm thì chắc nó ở nửa sau hoặc nửa đầu rồi” - Chính là Binary Search (Tìm kiếm nhị phân)
Khi sử dụng cách này thì phải đảm bảo điều kiện là dữ liệu của chúng ta đã được sắp xếp (theo bất kì kiểu gì)
Tư tưởng thuật toán này đi từ phần tử giữa của dữ liệu hiện tại. Khi mảng hiện tại được chia làm hai thì chỉ có 3 khả năng duy nhất:
 Ví dụ: A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9}; // Điều kiện đã được sắp xêp
Ví dụ: A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9}; // Điều kiện đã được sắp xêp
Key = 1
Các bước thuật toán như sau:
Code:
Mục lục
Giới thiệu bài toán
Thuật toán truyền thống
Tối ưu
Giới thiệu bài toán
Trong thực tế nhiều trường hợp, chúng ta luôn phải sắp xếp, tìm kiếm theo một chuẩn nào đó. Ví dụ như:
- Trong lớp có duy nhất một bạn được 9 điểm, hãy tìm bạn đó? Hay là một dãy sinh viên trong lớp tìm một sinh viên bất kì?
Truyền thống Linear Search
Tất cả chúng ta đều biết rằng, muốn tìm kiếm một sinh viên nào đó trên bảng danh sách thì cách đơn giản nhất đó là : “Đi từng sinh viên từ đầu, kiểm tra xem đó có phải sinh viên cần tìm không, không thì next”.
Ví dụ chúng ta có mảng A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9} với Key = 7
Theo đúng cách trên thì ta có cách duyệt từ đầu đến cuối. Nếu giá trị mình cần tìm là Key thì sẽ in ra vị trí xuất hiện đó

#include <iostream>
using namespace std;
int timKiem(int Arr[], int n, int Key) {
for (int i = 0; i < n; i++) {
if (Arr[i] == Key) {
return i; // tìm thấy thì sẽ kết thúc luôn
}
}
return -1;//tức không tìm thấy
}
int main() {
int A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int n = sizeof(A)/sizeof(int);
if (timKiem(A, n, 7) != -1) {
cout << "Tim thay 7 o vi tri " << timKiem(A, n, 7);
}
if (timKiem(A, n, 10) != -1) {
cout << "Tim thay 7 o vi tri " << timKiem(A, n, 7);
} else {
cout << "Trong mang khong ton tai so 10";
}
}
Cách tối ưu
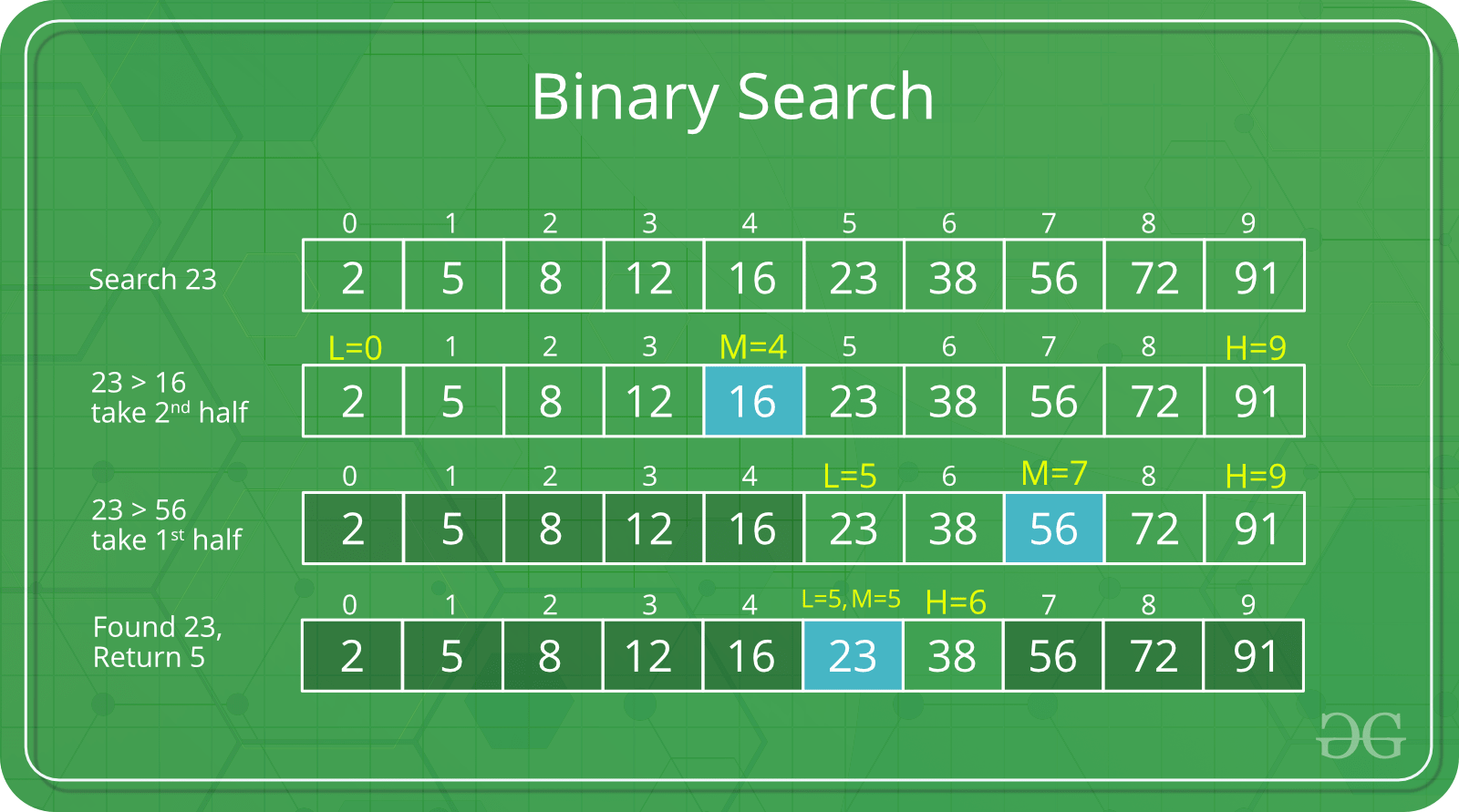
Về thuật toán tối ưu sự tìm kiếm thì có một thuật toán kiểu : “À mày không phải cái ta tìm kiếm thì chắc nó ở nửa sau hoặc nửa đầu rồi” - Chính là Binary Search (Tìm kiếm nhị phân)
Khi sử dụng cách này thì phải đảm bảo điều kiện là dữ liệu của chúng ta đã được sắp xếp (theo bất kì kiểu gì)
Tư tưởng thuật toán này đi từ phần tử giữa của dữ liệu hiện tại. Khi mảng hiện tại được chia làm hai thì chỉ có 3 khả năng duy nhất:
- Phần tử tìm kiếm là ở vị trí giữa
- Nếu không phải ở giữa thì nếu A[giữa] > Key tức là từ giữa->cuối đều > Key nên ta sẽ chỉ thao tác với mảng bên trái.
- Tương tự với mảng bên phải
 Ví dụ: A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9}; // Điều kiện đã được sắp xêp
Ví dụ: A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9}; // Điều kiện đã được sắp xêpKey = 1
Các bước thuật toán như sau:
- Khởi tạo Left=0, Right = n;
- Nếu Left <= Right thì tiếp tục thuật toán
- Lấy vị trí giữa là (10 - 0)/2 = 5 | A[mid] = 6
- So sánh thấy 1 < 6 nên sẽ thao tác với mảng bên trái. Lúc này Right của mảng sẽ là Right = mid - 1;
- Lấy lại mid = (Right-Left)/2 = 2 | A[mid] = 3
- So sánh thấy 1 < 3 nên sẽ thao tác với mảng bên trái. Right mới Right = mid-1 = 2
- Lấy lại mid = (Right-Left)/2 = 1 | A[mid] = 2
- So sánh thấy 1 < 2 nên sẽ thao tác với mảng bên trái. Right mới Right = mid-1 = 0
- Lấy lại mid = (Right-Left)/2 = 0 | A[mid] = 1
- Thấy Key == A[mid] ==1 nên sẽ dừng thuật toán => mid là vị trí cần tìm (0)
Code:
#include <iostream>
using namespace std;
int timKiem(int Arr[], int n, int Key) {
int left = 0, right = n; // Khởi tạo đầu đuôi
while(left<=right) {
int mid = (right - left)/2; // Khởi tạo vị trí giữa
if (Arr[mid] == Key) {
return mid; // Trả về vị trí tìm thấy key
} else if (Arr[mid] > Key) {
right = mid-1; // Tìm kiếm bên trái
} else if (Arr[mid] < Key) {
left = mid+1;//Tìm kiếm bên phải
}
}
return -1; //Nếu không tìm thấy
}
int main() {
int A[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int n = sizeof(A)/sizeof(int);
if (timKiem(A, n, 7) != -1) {
cout << "Tim thay 7 o vi tri " << timKiem(A, n, 7);
} else {
cout << "Trong mang khong ton tai so 7";
}
if (timKiem(A, n, 10) != -1) {
cout << "Tim thay 7 o vi tri " << timKiem(A, n, 7);
} else {
cout << "Trong mang khong ton tai so 10";
}
}


Nhận xét
Đăng nhận xét